Fórmula cuadrática
De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática3 a la ecuación que proporciona las raíces de la ecuación cuadrática:
 ,
,
donde el símbolo ± indica que los valores
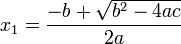
y 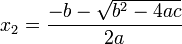
constituyen las dos soluciones.
[editar]Discriminante
En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):
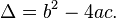
Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real demultiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.
- Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las abscisas: X):
-
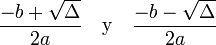 .
.
- Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X):
- Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):
- donde i es la unidad imaginaria.
En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.
[editar]Ecuación bicuadrática
Expresada de modo más general, una ecuación cuadrática en  es de la forma:
es de la forma:
 es de la forma:
es de la forma:
con n un número natural y a distinto de cero. El caso particular de esta ecuación donde n = 2 se conoce como ecuación bicuadrática.
[editar]Clasificación
La ecuación de segundo grado se clasifica de la manera siguiente:[cita requerida]
1. Completa. Es la forma canónica:
donde las tres literales: a, b y c, son distintas de cero.
Esta ecuación admite tres maneras para las soluciones: 1) dos números reales y diferentes; 2) dos números reales e iguales (un número real doble); 3) dos números complejosconjugados, según el valor del discriminante
ya sea positivo, cero o negativo, respectivamente.
Se resuelven por factorización, o por el método de completar el cuadrado o por fórmula general. Esta fórmula se deduce más adelante.
2. Incompleta pura. Puede expresarse de las dos maneras siguientes:
donde los valores de a y de c son distintos de cero. Se resuelve despejando x mediante operaciones inversas. Su solución son dos raíces reales que difieren en el signo si los valores de a y de c son de signo contrario, o bien dos números imaginarios puros que difieren en el signo si los valores de a y de c son del mismo signo.
Una ecuación cuadrática incompleta:
con a distinto de cero. Prácticamente aparece muy raras veces. Por supuesto, su única solución de multiplicidad dos es x = 0.
3. Incompleta mixta. Se expresa así:
donde los valores de a y de b son distintos de cero. Se resuelve por factorización de x. Siempre su solución es la trivial x1 = 0. En números imaginarios no hay solución.
[editar]Deducción para resolver la ecuación de la forma 
La ecuación de segundo grado se puede simplificar dividiendo por el coeficiente líder, de forma que
Si usamos otras letras para simplificarlo de forma que  y
y  la demostración (que es algo más sencilla) queda como sigue:
la demostración (que es algo más sencilla) queda como sigue:
 y
y  la demostración (que es algo más sencilla) queda como sigue:
la demostración (que es algo más sencilla) queda como sigue:
Desde la ecuación
Transponiendo n
Sumando  a ambos términos
a ambos términos
 a ambos términos
a ambos términos
Simplificamos el primer término a un binomio cuadrado
Extrayendo la raíz cuadrada a los dos miembros
Transponiendo 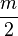 y simplificando la fraccion de la raíz
y simplificando la fraccion de la raíz
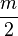 y simplificando la fraccion de la raíz
y simplificando la fraccion de la raíz
Simplficando a común denominador
si deshacemos el cambio de variables, obtenemos el resultado

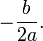
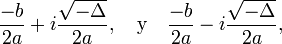







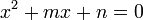




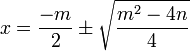

esta muy importante por que nos podemos guiar con estos problemas para poder resolver muchos mas.
ResponderEliminarsu blog les quedo muy bien en presentacion e informacion. ¡¡¡¡FELICIDADES!!!!
ResponderEliminarmuchas gracias también el tuyo esta muy bien realizado
ResponderEliminar