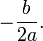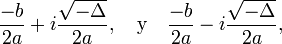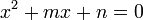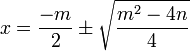matematicas: 2012

Realiza la siguiente ecuación por el método de eliminación gaussiana :

x+2y+3z=1

4x+5y+6z=-2

7x+8y+10z=5

Fórmula cuadrática

De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática³ a la ecuación que proporciona las raíces de la ecuación cuadrática:

$x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}$ ,

donde el símbolo ± indica que los valores

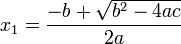
$x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a}$

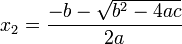
$\ x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a}$

constituyen las dos soluciones.

[editar]Discriminante

Ejemplo del signo del discriminante:
■ < 0: no posee soluciones reales;
■ = 0: posee una solución real (multiplicidad 2);
■ > 0: posee dos soluciones reales distintas.

En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con el símbolo Δ (delta):

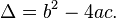
$\Delta = b^2 - 4ac.\,$

Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real demultiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.

Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje de las abscisas: X):

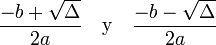$\frac{-b + \sqrt {\Delta}}{2a} \quad\text{y}\quad \frac{-b - \sqrt {\Delta}}{2a}$ .

Una solución real doble si el discriminante es cero (la parábola sólo toca en un punto al eje de las abscisas: X):

$-\frac{b}{2a} . \,\!$

Dos números complejos conjugados si el discriminante es negativo (la parábola no corta al eje de las abscisas: X):

$\frac{-b}{2a} + i \frac{\sqrt {-\Delta}}{2a}, \quad\text{y}\quad \frac{-b}{2a} - i \frac{\sqrt {-\Delta}}{2a},$

donde i es la unidad imaginaria.

En conclusión, las raíces son distintas si el discriminante es no nulo, y son números reales si –sólo si– el discriminante es no negativo.

[editar]Ecuación bicuadrática

Expresada de modo más general, una ecuación cuadrática en $x^n\,$ es de la forma:

$ax^{2n} +bx^n + c = 0 \,$

con n un número natural y a distinto de cero. El caso particular de esta ecuación donde n = 2 se conoce como ecuación bicuadrática.

[editar]Clasificación

La ecuación de segundo grado se clasifica de la manera siguiente:^{[cita requerida]}

1. Completa. Es la forma canónica:

$ax^2 + bx + c = 0 \,$

donde las tres literales: a, b y c, son distintas de cero.

Esta ecuación admite tres maneras para las soluciones: 1) dos números reales y diferentes; 2) dos números reales e iguales (un número real doble); 3) dos números complejosconjugados, según el valor del discriminante

$\Delta = b^2 - 4ac \,$

ya sea positivo, cero o negativo, respectivamente.

Se resuelven por factorización, o por el método de completar el cuadrado o por fórmula general. Esta fórmula se deduce más adelante.

2. Incompleta pura. Puede expresarse de las dos maneras siguientes:

$ax^2 + c = 0 \,$

donde los valores de a y de c son distintos de cero. Se resuelve despejando x mediante operaciones inversas. Su solución son dos raíces reales que difieren en el signo si los valores de a y de c son de signo contrario, o bien dos números imaginarios puros que difieren en el signo si los valores de a y de c son del mismo signo.

Una ecuación cuadrática incompleta:

$ax^2 = 0 \,$

con a distinto de cero. Prácticamente aparece muy raras veces. Por supuesto, su única solución de multiplicidad dos es x = 0.

3. Incompleta mixta. Se expresa así:

$ax^2 + bx = 0 \,$

donde los valores de a y de b son distintos de cero. Se resuelve por factorización de x. Siempre su solución es la trivial x₁ = 0. En números imaginarios no hay solución.

[editar]Deducción para resolver la ecuación de la forma $a x^2+bx+c = 0$

La ecuación de segundo grado se puede simplificar dividiendo por el coeficiente líder, de forma que

$ax^2+bx+c=0 \ \Leftrightarrow \ x^2 + \frac{b}{a}x + \frac{c}{a} = 0$

Si usamos otras letras para simplificarlo de forma que $m = \frac{b}{a}$ y $n = \frac{c}{a}$ la demostración (que es algo más sencilla) queda como sigue:

Desde la ecuación

$x^2+mx+n=0 \,$

Transponiendo n

$x^2 + mx = -n \,$

Sumando $\frac{m^2}{4}$ a ambos términos

$x^2+mx+\frac{m^2}{4}=\frac{m^2}{4}-n$

Simplificamos el primer término a un binomio cuadrado

$\left( x+\frac{m}{2} \right)^2=\frac{m^2}{4}-n$

Extrayendo la raíz cuadrada a los dos miembros

$x+\frac{m}{2} = \pm \sqrt{\frac{m^2}{4}-n}$

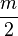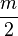Transponiendo $\frac{m}{2}$ y simplificando la fraccion de la raíz

$x = \frac{-m}{2}\pm \sqrt{\frac{m^2 - 4n}{4}}$

Simplficando a común denominador

$x = \frac{-m \pm \sqrt{m^2-4n}}{2}$

si deshacemos el cambio de variables, obtenemos el resultado

$x = \frac{-b \pm \sqrt{b^2 - 4ac} }{ 2a }$

matemáticas

El término matemáticas viene del griego "máthema", que quiere decir aprendizaje, estudio y ciencia. Y justamente las matemáticas son una disciplina académica que estudia conceptos como la cantidad, el espacio, la estructura y el cambio. El alcance del concepto ha ido evolucionando con el tiempo, desde el contar y calcular hasta abarcar lo mencionado anteriormente. Aunque algunos las consideran como una ciencia abstracta, la verdad es que no se puede negar que esta inspirada en las ciencias naturales, y uno de sus aplicaciones más comunes se lleva a cabo en la Física.

La historia de las matemáticas comienza con la primera gran "abstracción", que es el desarrollo de los números y el contar. Los orígenes de esta disciplina vienen dados por una necesidad bastante básica: la necesidad de contar objetos físicos para el comercio (en sus inicios el trueque), para clasificar extensiones de territorio y para realizar asociaciones relacionadas con los astros. Por supuesto que la siguiente necesidad fue la de realizar operaciones básicas con estos números, para poder hacer predicciones básicas: el sumar, restar, multiplicar y dividir. Además, paralelamente se desarrollaron los conceptos geométricos, de los cuales tenemos pruebas sólidas como los antiguos monumentos monolíticos.

El siguiente gran paso en la historia de las matemáticas viene dado por el desarrollo de sistemas de notación o escritura. Los sistemas desarrollados han sido de una gran variedad, desde el uso de nudos en cuerdas hasta la utilización de conceptos más abstractos como los números que usamos en la actualidad. Un gran paso en este sentido viene dado por la invención del cero en la India.

La refinación de todos estos conceptos básicos lo podemos ver a través de la línea del tiempo en todas las culturas, en libros provenientes de la antigua India, Egipto, Mesopotamia y Grecia. Posteriormente, en el siglo XVI, mediante la interacción entre los nuevos descubrimientos científicos y las matemáticas, es que el desarrollo de la disciplina se vio ampliamente acelerado, llegando a ser una de las fundaciones del conocimiento científico que poseemos hoy en día. De hecho cuando hablamos de "matemáticas aplicadas", nos referimos al uso de las mismas en el contexto específicos de las diversas ciencias, y también en relación con otros ámbitos.

Ahora revisaremos algunos conceptos interesantes. La lógica: Este es un campo que se ocupa de sistemas formales para establecer de manera intuitiva objetos matemáticos como números, computaciones (procesamiento de la información), demostraciones y conjuntos. Las funciones matemáticas: Una función matemática relaciona cada uno de sus elementos con un resultado o elemento de salida. Por ejemplo la función f(x)=2x, se refiere a que el elemento x, por ejemplo 3, tiene como resultado o salida al 6, o sea f(3)=6. Las fórmulas matemáticas: la fórmula matemática es información simbólica que determina una relación entre cantidades (por ejemplo la famosa fórmula de Einstein E=mc²). La inducción: Es un método de demostración o prueba, para establecer si una determinada aseveración es válida para todos los números naturales (0, 1, 2, 3...).

En la actualidad las matemáticas nos acompañan silenciosamente tras todos los artefactos que utilizamos, las construcciones en las que nos movemos, en nuestros autos y aviones. Las matemáticas, al igual que el lenguaje, más que un invento son la expresión de potencialidades propias del cerebro humano; en palabras simples podemos decir que la naturaleza misma desea que las utilicemos.

jueves, 13 de diciembre de 2012